研究紹介

過去の研究テーマ

SiCデバイスの応力解析と順方向劣化現象への応力の影響

ワイドギャップ半導体である炭化ケイ素(SiC)は、Si半導体以上の電気特性を有することから次世代パワーデバイスの材料として注目されています。半導体デバイスには，その製造過程で複雑な応力分布が生じ，信頼性低下を引き起こす原因となります。加えて，バイポーラデバイスでは，順方向劣化現象と呼ばれる通電により積層欠陥が拡大する特異な現象が生じ，デバイスへの大きな課題となっています。本研究では，特に開発が盛んな4H-SiCパワーデバイスの信頼性向上を目的に，応力分布解析手法の構築や，順方向劣化現象に応力が与える影響のモデル化を行っています。

半導体に生じる応力は，実験的にはラマン分光法によりラマンシフトと呼ばれる光の振動数の変化を測定することで評価ができます。しかしながら，ラマン分光法のみで6成分ある応力を決定することはできません。そこで，デバイス製造プロセスを再現する有限要素法（FEM）を行ってデバイスの応力分布を求め，実験との比較によりFEM解析の妥当性を確認するという手法を4H-SiCに適用し，デバイスの応力分布を成分毎に分解して明らかにする手法を開発しました[1]。

また，SiCバイポーラデバイスの順方向劣化現象に対して，信頼性確保に必要となる定量的な理論モデルの構築のため，順方向劣化現象に応力が与える影響のモデル化を行っています。通電実験，デバイスシミュレーション（TCAD），FEM解析を組み合わせる事により，順方向劣化現象の判定基準となる閾値キャリア密度にデバイスに加わる応力が与える影響をモデル化に成功しました[2]。

参考文献

1. H. Sakakima, S. Takamoto, Y. Murakami, A. Hatano, A. Goryu, K. Hirohata, and S. Izumi, “Development of a method to evaluate the stress distribution in 4H-SiC power devices”, Japanese Journal of Applied Physics 57, 106602 (2018).
2. H. Sakakima, A. Goryu, A. Kano, A. Hatano, K. Hirohata, and S. Izumi, “Modeling the effect of mechanical stress on bipolar degradation in 4H-SiC power devices”, Journal of Applied Physics 128, 250701 (2020).

SiC結晶の強度、結晶欠陥の原子スケールモデリング

デバイスの機械的信頼性を確保，向上させるためには，デバイスを構成する材料自体の理解が不可欠です．そのため，材料の機械的特性や結晶欠陥を対象とした第一原理計算や分子動力学法を用いた研究も多く行っています．SiCパワーデバイスの信頼性に対して大きな課題となっている積層欠陥に関連し，これまでに第一原理計算による積層欠陥エネルギーの温度依存性の解析 [1]や，異なる汎関数を使用した場合の予測精度の評価[2]，余剰キャリアの存在による積層欠陥エネルギーの変動[3]等を調査してきました．また，現在は材料強度そのものに対して余剰キャリアが与える影響[4]に注目した解析を進めています．

参考文献

1. H. Sakakima, S. Takamoto, A. Hatano, and S. Izumi, “Temperature-dependent stacking fault energies of 4H-SiC: A first-principles study”, Journal of Applied Physics 127, 125703 (2020).
2. H. Sakakima, A. Hatano, S. Izumi, “Comparative study of the effect of van der Waals interactions on stacking fault energies in SiC”, Journal of Applied Physics 130, 215701 (2021)
3. H. Sakakima and S. Izumi, “First-principles investigation of the effects of excess carriers on the polytype stability and stacking fault energies of SiC,” Journal of Applied Physics 134, 155103 (2023).
4. H. Sakakima, S. Izumi, “Carrier-doping effect on strength and deformations in group-IV crystals,” International Journal of Mechanical Sciences 293,110169 (2025).

4H-SiCにおけるBPD-TED変換現象解明のための反応経路解析

次世代のパワーデバイス用材料として近年着目されている4H-SiCの課題の1つとして、基底面転位(BPD)と呼ばれる転位が存在することが挙げられます。この転位はデバイス性能を著しく低下させることから、成膜時に大部分のBPDは貫通刃状転位(TED)と呼ばれる良性の転位に変換させています。しかしながら、BPD-TED変換現象は表面付近で起こる複雑な現象であることから、変換メカニズムは明らかになっていません。そこで本研究では、変換メカニズムを分子動力学から解明することを目的としています。

BPDは部分転位に別れて存在しており、表面付近で1本の完全転位へと収縮し、交差すべりによってTEDへ変換されると考えられています。そこでまず初めに、らせんBPDの収縮に表面が与える影響を解明するために、転位移動時のNEB法による反応経路解析を行いました。反応経路解析を行うことで、転位が移動するときの活性化エネルギーを見積もることができます。表面から転位対までの深さごとに、転位対が収縮する時、拡張する時の活性化エネルギーを算出し比較することで、表面から転位対までの距離がどのようなときに収縮が起こりやすい/起こりづらいのかが分かります。解析の結果、表面極近傍では部分転位の収縮が起こりやすいということが分かりました。次に、完全転位となったBPDからTEDへと交差すべりする過程について、反応経路解析を行ったところ、表面付近では交差すべりが即座に起こることが分かりました。このことから、BPD-TED変換には表面からの距離が大きく影響するということが示唆されます。

最後に、BPDがTEDへと変換される過程についてMDシミュレーションを行ったところ、これらの解析で明らかになったように、表面から変換されていく様子が確認できました。

反応経路解析によって得られたエネルギー曲線の一例

参考文献

1. Yohei Tamura, Hiroki Sakakima, So Takamoto, Asuka Hatano, Satoshi Izumi, “Reaction pathway analysis for the conversion of perfect screw basal plane dislocation to threading edge dislocation in 4H-SiC”, Jpn. J. Appl. Phys. 58 081005 (2019)
2. Atsuo Hirano, Hiroki Sakakima, Asuka Hatano, Satoshi Izumi, “Reaction pathway analysis for the contraction of 4H-SiC partial-dislocations pair in the vicinity of surface”, Jpn. J. Appl. Phys. 60 085502 (2021)
3. Atsuo Hirano, Hiroki Sakakima, Asuka Hatano, Satoshi Izumi, “Charge-transfer interatomic potential to reproduce 30° partial dislocation movements for 4H-SiC in the surface vicinity and its application to BPD‒TED conversion,” Computational Material Science 231, 112588 (2024).
4. Atsuo Hirano, Hiroki Sakakima, Asuka Hatano, Satoshi Izumi, “Long-range Tersoff potential for silicon to reproduce 30° partial dislocation migration,” Computational Material Science 231, 112557 (2024).
5. Atsuo Hirano, Hiroki Sakakima, Asuka Hatano, Satoshi Izumi, “Effects of terraces and steps on the 4H-SiC BPD-TED conversion rate: A reaction pathway analysis”, Journal of Applied Physics 135, 095701 (2024).

分子動力学シミュレーションの材料強度問題への適用

分子動力学を活用した研究も進めており，特に深層学習を活用した高精度な原子間ポテンシャルの活用や原子間ポテンシャルの開発に注目しています．近年，深層学習を活用した適用対象を問わない汎用の高精度原子間ポテンシャルが提案されています．これにより従来適用が困難であった現象へと分子動力学の適用範囲が大きく拡大することが期待されており，これを活用しこれまで適用が困難であった多元素が混在する材料の原子ネットワーク構造や機械特性の解析を進めています．現在は半導体デバイスの絶縁膜に多用されるSiO2に注目し，CやN元素が混入することによる機械的強度の変化やCクラスタと呼ばれるC原子の凝集挙動の解析を進めています。

参考文献

1. Hiroki Sakakima, Keigo Ogawa, Sakurako Miyazaki, Satoshi Izumi, “Exploration of the Mechanical Properties of Carbon-Incorporated Amorphous Silica Using a Universal Neural Network Potential,” Journal of Applied Physics 135, 085104 (2024).
2. Sakurako Miyazaki, Hiroki Sakakima, Keigo Ogawa, Satoshi Izumi, “Molecular Dynamics Study of the Effect of Composition on Elastic Properties of Silicon Oxynitride Films,” Japanese Journal of Applied Physics 63(11), 115502 (2024).

鉄道分岐器のフロントロッド付属軸受の摩耗予測

列車が分岐器のトングレール後端部に存在する継目を通過する際、レール継目部において衝撃振動が発生します。この衝撃振動がトングレールを経由してフロントロッドに伝わると、フロントロッドに付属する軸受が摩耗します。フロントロッドはトングレールの位置情報を電気転てつ機に伝達するための部品の一つであり、その軸受に摩耗が累積することは分岐器の転換不能の原因となります。本研究では、摩耗のメカニズムを明確にするために、衝撃応答特性を再現した普通分岐器と特殊分岐器の有限要素モデルを作成し、トングレール後端部に衝撃が入力された際の軸受における面圧と滑り速度を算出する解析を行いました。さらに、軸受の摩耗試験とその試験を再現する有限要素法解析から算出した比摩耗量を用いることで、フロントロッド付属軸受の摩耗量予測を行いました。

また現在は、このような衝撃振動がどのようなメカニズムによって発生するかを明らかにするために、小型カメラを用いた変位の測定に取り組んでいます。測定の結果、列車が通過した際には、トングレールがシーソー状の運動を行い、これによりトングレールと床板との衝突が発生することがわかりました。また有限要素解析により車輪がレール上を通過する様子を再現することで、衝撃振動の増幅にどの程度発生するか検証を行いました。また、このような衝撃増幅現象が肘金に与える影響を定量的に評価することで、部品のメンテナンスをより効率的に行うことが可能となります。

普通分岐器モデル概観

参考文献

• 近藤 祐樹, 島本 琢磨, 波田野明日可, 泉 聡志, 酒井 信介, 樋口 博俊, 鈴木 雅彦, 加藤 尚志, "車両通過時の衝撃振動による分岐器のフロントロッド摩耗予測のための有限要素モデリング", 日本機械学会論文集, Vol. 81, No. 832 (2015), DOI:10.1299/transjsme.15-00286.
• 島本 琢磨, 田處 恵大, 波田野 明日可, 泉 聡志, 酒井 信介, 新野 善行, 鈴木 雅彦, 金田 敏之, "列車通過時振動による特殊分岐器フロントロッド部品の摩耗予測のための有限要素モデリング", 日本機械学会論文集, Vol.85, No.873, pp.18-00414 (2019) DOI: 10.1299/transjsme.18-00414
• 重盛 壮平, 三浦 友裕, 榊間 大輝, 泉 聡志, 戸丸 耕太, 佐々木 和洋, 金田 敏之, "鉄道分岐器の転換動作時におけるフロントロッド軸受摩耗のマルチボディ解析（調整状態の影響）", 日本機械学会論文集, Vol.89, No.919, p. 22-00289 (2023) DOI:10.1299/transjsme.22-00289
• 三浦 友裕, 寺門 暉斗, 榊間 大輝, 泉 聡志, 戸丸 耕太, 佐々木 和洋, 金田 敏之, "小型カメラを用いた変位測定と有限要素解析による鉄道分岐器のトングレール継ぎ目における衝撃振動増幅現象の解明", 日本機械学会論文集, Vol.90, No.936, p. 24-00111 (2024) DOI: https://doi.org/10.1299/transjsme.24-00111

ボルト・ナット締結体の有限要素法解析～剛性・ゆるみへの問題適用

ボルト・ナット締結体のトラブルは21世紀を迎えた現代でも絶えることはありません。当研究室では、有限要素法解析（幾何学的非線形接触摩擦解析）により、ボルトのゆるみをシミュレーションすることに近年成功しました。現在では、締結体の剛性とゆるみのメカニズムについての理論的解明に至っています。当研究室ではこの技術を使って、企業との様々な共同研究を行ってきました。本技術を産業界にさらに移転するための相談・議論・共同研究の希望などを受け付けております。気軽にご相談ください。詳細は、ボルトの研究紹介ページをご覧ください。

鉄道車両構体の有限要素解析の機械学習代替モデル

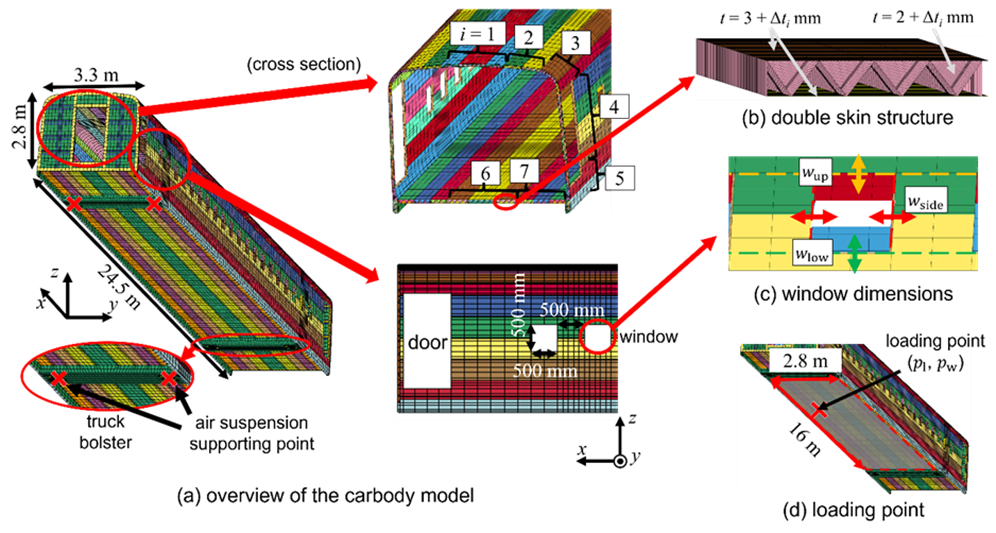
鉄道車両の主要構造である車両構体には、板材と骨組みを一体化した段ボール状の断面を有する“ダブルスキン構造”が広く採用されています。設計初期段階では、ダブルスキン構造を構成する形材の厚みや窓の寸法、床下機器の配置などの設計変数を変更しながら有限要素解析を繰り返し、所望の水準を満たす設計変数を選定します。しかし、巨大かつ複雑な構造をもつ車両構体の場合、こうした一連の工程には多大な計算負荷・時間を要するだけでなく、解析前の形状変更やメッシングにも作業時間を要します。

本研究では、このような形状や条件の頻繁な変化を伴う問題における負担低下を目的に、機械学習を用いた代替モデル（サロゲートモデル）の開発に取り組んでいます。代替モデルは、入力変数と出力変数の関係を近似的に定義、学習することで、計算負荷の高い数値計算を行わずに入力から直接出力（予測結果）を算出する手法です。これまでに構築した代替モデルを用いることで、車両構体設計で重要となる上下1次曲げ振動に関して、分布荷重に対する最大たわみ、変形・応力分布、固有振動数および固有モードを、有限要素解析を実行せずに予測できることを確認しています。

参考文献

• 福元 康平，榊間 大輝，古谷 了，川崎 健，泉 聡志，主成分分析と多層パーセプトロンを用いた鉄道車両構体の有限要素解析の機械学習代替モデル，日本機械学会論文集，Vol.90, No.937(2024),DOI:10.1299/transjsme.24-00133

鉄道車両のボルト締結部における有限要素簡易モデルの作成

ボルト締結は鉄道車両等の幅広い機械構造物に使用されていますが、締結部は強度的な弱点となることが多いため、強度・振動特性の観点から十分な信頼性の確保が要求されています。しかし、多数のボルト締結を用いる構造物の設計に対して全てのボルト締結を詳細にモデル化することは、計算負荷の観点から現実的ではないため、簡素かつ高精度なモデルが求められています。

そこで、まずは基礎的検討として平板継手の簡易モデル化手法を提案しました。ボルト締結をビーム要素、被締結部材をシェル要素でモデル化し、ボルト締結によって圧縮力が伝播する領域（等価座面領域）を剛体拘束や補間剛体要素によって拘束することで、締結部近傍の並進剛性やひずみ分布、固有振動数を高精度に再現しました。

さらに、簡易モデリング手法を艤装レールボルト締結体へと応用しました。平板継手の場合と同様、ボルト締結をビーム要素、その他の部材をシェル要素でモデル化し、その等価座面領域を拘束することで高精度に並進剛性とひずみ分布、固有振動数を予測しました。

平板継手の有限要素簡易モデル

参考文献

• 上田亮，吉村侯泰，馬場輝明，中村英之，川崎健，福元康平，榊間大輝，泉聡志，「鉄道車両の艤装用ボルト締結継手に対する補間剛体要素を用いた有限要素簡易モデルの開発」，日本機械学会論文集，日本機械学会，90(936), 24-00049 (2024).

ワイヤロープの有限要素モデリング

《エレベータ用ワイヤロープ》

エレベータ用ワイヤロープ8×S(19)の軸方向剛性と径方向剛性を再現する有限要素モデリング手法の開発を行いました。また、径方向の剛性については、ストランド、心綱、ワイヤロープの径方向剛性の計測法を新たに提案しています。

初めに、ストランドの径方向圧縮実験により、ストランドの径方向剛性（みかけのヤング率 20 GPa）は、軸方向（みかけのヤング率 150 GPa）に比べて小さいことがわかりました。径方向荷重により、ストランド間の接触が強固になり、隙間が埋まり、充填率が上がると、剛性が高まることが実験及び解析両面からわかりました。このことから、素線間の接触の密着度の再現が有限要素モデリングにおいて重要であることがわかりました。開発した有限要素モデルはストランドの軸方向及び径方向の剛性を再現しています。

次に、心綱の径方向圧縮実験により、心綱の径方向剛性は、繊維の特性を反映して、ヒステリシスを有することがわかりました。心綱が圧縮された状態からの除荷直後の剛性のみを再現するため、有限要素モデルでは、心綱のヤング率を300 MPaに設定しています。

最後に、ワイヤロープの径方向圧縮実験により、ワイヤロープの径方向剛性は、心綱の特性を反映し、ヒステリシスを有し、みかけのヤング率も心綱とほぼ等しいことがわかりました。また、ロープにかかる張力に依存し、張力が大きいほど高くなることがわかりました。これは張力により素線間、心綱ーストランド間の接触状態が強固になるためと考えられます。有限要素モデルでは、ストランドが食い込んだ実物の心綱の形状を再現したワイヤロープのモデルを作成し、軸方向剛性及び径方向剛性が実験をおおよそ再現することがわかりました。

《クレーン用ワイヤロープ》

クレーン用ワイヤロープIWRC 6×Fi(29)についても有限要素モデルを作成しました。IWRC 6×Fi(29)はエレベータ用ワイヤロープと違って心綱が鋼製であることから内部状態が大きく異なります。ロープ内部における素線間の接触点が多いことから内部摩擦の影響が大きく、より高い内部素線接触状態の再現性が要求されます。

軸方向引張試験・径方向圧縮試験とそれらを再現する解析結果の比較により、ストランド・鋼心・ロープ全体のそれぞれについて実際の剛性をモデルはよく再現することを確認しました。このモデルを用いて、実際の運用における滑車に巻き取られる使用状況を模擬した解析を行って素線の疲労を評価したところ、実際の疲労試験で断線が多く確認される素線において高い応力振幅が発生しており、疲労損傷の可能性が高いことが明らかになりました。

開発したエレベータ用ワイヤロープ8×S(19)の有限要素法モデル

開発したクレーン用ワイヤロープIWRC 6×Fi(29)の有限要素法モデル

参考文献

• 泉 聡志，中谷 起也，太田 仁衣奈，波田野 明日可，山際 謙太, “エレベータ用ワイヤロープの径方向剛性を再現する有限要素モデリング”,日本機械学会論文集、Vol. 87, No. 896 (2021) DOI: 10.1299/transjsme.20-00418
• 山際 謙太， 緒方 公俊， 泉 聡志, “ワイヤロープの疲労試験と有限要素解析”,日本機械学会誌、124巻1237号 (2021) P24-27　WEB
• 緒方 公俊，山口 篤志， 山際 謙太， 佐々木 哲也， 泉 聡志, “素線形状の幾何学的定式化によるワイヤロープ断面内の断線位置推定手法の提案”,日本機械学会論文集、Vol. 88, No. 908 (2022) 22-00038　WEB
• 太田 仁衣奈，緒方 公俊，山際 謙太，泉 聡志, “IWRCワイヤロープの有限要素モデリングによる軸方向と径方向剛性の再現”,日本機械学会論文集、Vol. 88, No. 913 (2022)22-00144 WEB

粘着剤ーシリコンウェハ間の剥離現象の分子動力学解析

半導体製造工程における搬送時の支持部材やシリコンウェハの保護材として使用される粘着テープについて，シリコンウェハに貼付された粘着テープの接着強さなどの特性を明らかにするために分子動力学法を用いて剥離シミュレーションモデルを構築した．粘着剤とアモルファスSiO2(被着体)の圧着時間，被着体の表面粗さ，分子量の異なる粘着剤など複数のモデルに対して，剥離シミュレーションを行い，粘着剤の接着強度（剥離応力の最大値）や剥離エネルギーについて定量化をおこなった．

最初に，シリコンウェハ（表層のアモルファスSiO2）と粘着剤構成原子間に働くvan der Waals力（Lennard-Jones型）を密度汎関数計算(Density of Functional Theory)で算出し，アモルファスSiO2と粘着剤原子間のσ（原子間距離）とε(エネルギー係数)の合わせ込みを行い，分子動力学(Molecular Dynamics)で使用する力場パラメータを作成した．結果として，DFTとMDの間が20%の範囲で一致しており，妥当な結果であることを述べた．

次に作成したMDの力場パラメータを用いて，粘着剤とシリコンウェハを接合し，計算条件を変更して剥離シミュレーションを行った．１つ目は粘着剤の圧着時間が増えることでアモルファスSiO2と結合状態にある原子の数が増えていく経過について説明した．結合状態にある原子対の数では表面粗さの依存性が明確に示されなかったが，アモルファスSiO2と粘着剤間の結合エネルギーで評価したところ，表面粗さに対して明確な差が現れた．これはアモルファスSiO2が3次元的に配置されることで結合を強くさせる効果が大きいためと考えられる．特にクーロンエネルギーよりもvan der Waals力の影響が高くなることについて述べた．また，結合原子対の数をパラメータにして最大応力の値と剥離エネルギーを算出したところ，表面粗さが増大すると剥離応力の最大値および剥離エネルギーは増加することが示された．最も表面粗さの大きいRMS10Åで計算したモデルでは剥離応力や剥離エネルギーがRMS0,2,5Åのモデルと比べて大きく上昇することから，表面粗さの影響で結合が三次元的になり，さらに強度が上がっていると考えられる．

最後に，分子量と架橋構造を変えた粘着剤モデルを用いて剥離シミュレーションを行った(Figure 1)．その際，粘着剤の架橋構造を40本ある部分鎖を一つの箱で表し，つながっている部分鎖同士を線でつなぎ，粘着剤を変位させる基板に拘束されている部分鎖に対しては枠の色を変えて表示し，アモルファスSiO2と結合状態にある場合にはその結合原子対の数を表記する独自のネットワーク図を作成した．このネットワーク図を利用することで，粘着剤の構造と剥離時の挙動が追跡可能であることを新たに示した（Figure 2）．さらにこのネットワーク図と，アモルファスSiO2と結合した部分鎖が剥離の進展とともに結合原子対の数が増減するグラフを作成し、剥離プロセスの詳細解析を可能にした．剥離エネルギーについては，粘着剤の分子量が大きくなると増えることが分かった．これは剥離に寄与する粘着剤原子の数が増え，粘着剤が完全に剥離するまでに必要なエネルギーも増えるためと考えられる．一方で剥離応力の最大値については，40本ある部分鎖の初期座標が同じで，架橋後の分子量のみが異なる３つのモデルで比較したところ，剥離応力の最大値は分子量に依存しなかった．粘着剤の分子鎖の配置や架橋構造について上記ネットワーク図と結合原子対の増減グラフを用いて分析したところ，剥離応力が最大となる付近で，シリコンウェハと結合している部分鎖の本数が多いほど剥離応力の最大値が大きくなることが明らかになった．そこで40本ある部分鎖の初期座標が異なる粘着剤モデルを追加で構築し，（初期構造3種類）×（分子量3種類）＝（9種類のモデル）で剥離シミュレーションをおこない，剥離応力の最大値を平均値で比較したところ，分子量が大きいモデルの方が，平均の剥離応力の最大値が大きくなることを述べた．同一の分子量間におけるバラツキを確認したところ，分子量の大きいモデルの方が架橋構造・配置に対する場合の数が増えることから，剥離応力の最大値のバラツキが大きいことを述べた．

Figure 1 Adhesive peeling model

Figure 2 Network Diagram of adhesive

参考文献

• 岩方 裕一, 泉 聡志, 分子動力学法による粘着剤－シリコンウェハ間のはく離現象への粘着剤の分子量が及ぼす影響，材料 71-2, 143-150(2022).  https://doi.org/10.2472/jsms.71.143
• 岩方 裕一, 泉 聡志, 分子動力学シミュレーションによるSiウェハと感圧性接着剤の相互作用と剥離挙動の研究, 日本接着学会誌, 57-10, 397-404(2021)

時間・空間スケールをつなぐマルチスケールシミュレーションの開発と材料強度問題への応用

有限要素法・転位動力学・分子動力学・電子状態計算を組み合わせたマルチスケールシミュレーションの開発を行っています。特に、時間スケールと空間スケールのギャップの問題を克服する手法開発に主眼を置いています。開発されたシミュレータは、半導体分野や電子デバイス分野の転位生成／進展現象・剥離現象などに応用されています。マクロスケール（連続体）とナノスケール（原子系）をつなぐためには、mからnm、secからnsecまでの9桁のギャップを克服しなけばなりません。空間スケールの克服のためには、有限要素法－分子動力学シミュレータを開発し、薄膜の剥離問題へと適用しています。Fig.1はナノインデンテーションによる薄膜の剥離試験モデルで、下部が有限要素法でモデル化されています。Fig.2は、計算結果であり、実験と同様の位置で剥離が起こっています[1]。時間スケールの克服のためには、Nudged Elastic Band法に基づいた反応経路探索の手法開発と応用を行っています。Fig.3は、シリコンのコーナーからの転位生成問題へ適用した例で臨界応力時（Athermal stress）の転位発生例です[2]。Fig.4は、転位生成の活性化エネルギの応力依存曲線であり、正解で初めて、Shuffle-set転位（(111)面の広いほうの平面に位置する転位）とGlide-set転位（(111)面の狭いほうの平面に位置する転位）の比較を可能にし、低温・高応力ではShuffle-set転位、高温・低応力ではGlide-set転位が生成する実験結果を理論的に支持する結果を得ました[3]。さらに、この結果を転位動力学と組み合わせることによって、その後の進展・増殖課程を扱うことが出来ます（Fig.5）[4]。

Fig.1 ナノインデンテーションによる薄膜の剥離試験のFEM-MDモデル

Fig.4 転位生成の活性化エネルギの応力依存曲線
（Glide-set転位とShuffle-set転位の違い）

参考文献

• [1] S. Hara, T. Kumagai, S. Izumi, S. Sakai, “Multiscale analysis on the onset of nanoindentation-induced delamination: Effect of high-modulus Ru overlayer”, Acta Materialia 57 (2009) pp. 4209-4216.
• [2] Satoshi. Izumi, Sidney. Yip, “Dislocation Nucleation from a Sharp Corner in Silicon”, J. Appl. Phys. 104 (2008) 033513.
• [3] K. Shima, S. Izumi and S. Sakai,“Reaction Pathway Analysis for Dislocation Nucleation from a Sharp Corner in Silicon: Glide Set versus Shuffle Set”, J. Appl. Phys., 108 (2010), 063504.
• [4] S. Izumi, T. Miyake, S. Sakai, H. Ohta, “Application of three-dimensional dislocation dynamics simulation to the STI semiconductor structure”, Materials Science Engineering A, 395,1-2 (2005) pp.62-69.

人体有限要素モデルによるアメリカンフットボール頭部衝突解析

アメリカンフットボールは激しい衝突を特徴とするスポーツ競技であり、アメリカンフットボールの発祥国である米国では圧倒的な人気を誇っている（福田，2020）。一方、その競技特性ゆえに、外傷発生件数も非常に多く（Dick et al., 2007; Hootman et al., 2007; 藤谷他, 2006, 2012）、特に脳震盪を始めとする頭部外傷は死亡事故や重篤な記憶障害を引き起こす事例も多数報告されている。
本研究では、THUMSが頭頚部中間位姿勢を保持できる頚部筋肉モデルの筋活性度条件を求め、頚部予備緊張状態を再現したアメリカンフットボール競技者の頭頚部有限要素モデルを作成した。作成した頭頚部有限要素モデルを用いてアメリカンフットボール競技中の頭部衝突を再現する有限要素解析を行い、頚部予備緊張を考慮したモデルの妥当性を確認すると共に、アメリカンフットボールの頭部衝突において頚部筋力及び頚部予備緊張が頭部キネマティクスに与える影響を評価した。

結果、頚部予備緊張を考慮したモデルでは考慮しないモデルと比較して、頭部衝突時の頭部キネマティクスが実人体を対象とした実験結果に近づくことが分かった。また、低負荷な頭部衝突に限った検討ではあるが、筋力トレーニングにより頚部筋力を強化することと、衝突を早く予期し衝突時の頚部筋筋活性度を高めることはいずれも、頭部重心角速度の増加量を減少させる効果があり、脳内に生じるひずみも減少させ、脳傷害の発生リスクを低減させることが示唆された。

人体衝撃の有限要素モデリング

参考文献

• 植田 章裕，今泉 俊介，中川恒大，藤本 圭一郎, 波田野 明日可, 泉 聡志, 酒井 信介, "有限要素法を用いた有人ロケット緊急離脱時における人体傷害評価及び脳傷害メカニズム解明", Transactions of the JSME (in Japanese), Vol. 84, No. 866 (2018) DOI: 10.1299/transjsme.18-00126
• 永長敬弘，榊間大輝，波田野明日可，原祥太郎，酒井 信介，泉聡志，"頚部予備緊張を考慮した人体有限要素モデルによるアメリカンフットボール頭部衝突解析"，日本機械学会論文集，日本機械学会，90(929)，23-00215 (2024).

固体間摩擦解析のためのMD解析手法の開発

自動車エンジンの燃費向上のため，ピストン－シリンダ間の摩擦損失の低減が必要とされています．特に固体間摩擦の低減のためには，ZnDTP(Zinc dialkyldithiophosphates)をはじめとする潤滑油添加剤の反応により摩擦面に形成されるトライボフィルムの役割が重要となります．しかし摺動中の摩擦面を実際に観察することが困難であるため，原子スケールの現象を扱うことができる分子動力学法(MD)の適用が求められています．

本研究では，ZnDTPトライボフィルムと酸化鉄をMDで扱うためのO-Fe-P-Zn系原子間ポテンシャルを作成し，摺動時に発生するトライボケミカル反応を対象としたシミュレーションを行いました．このような摩擦シミュレーションにより，接触圧力やZnDTPトライボフィルムの組成の違いなどが摺動時の現象に及ぼす影響や，摺動に伴うZnDTPトライボフィルムの構造変化を明らかにすることができます．下の動画は，ZnDTPトライボフィルム中に取り込まれた酸化鉄摩耗粉が分解される現象(摩耗粉の消化)を対象としたシミュレーションの結果です．摺動に伴う反応によって摩耗粉中の原子がZnDTPトライボフィルム中に拡散していく様子を再現しました．また摺動時のせん断応力やFeイオンの反応により，ZnDTPトライボフィルムの構造・特性が変化することを明らかにしました．

ZnDTPトライボフィルムに取り込まれた酸化鉄摩耗粉のモデル

参考文献

• H. Sakakima, T. Okazawa, K. Kume, S. Kobayashi, K. Kawaguchi, Y. Miyauchi, and S. Izumi, “Development of charge-transfer interatomic potential for O-Fe-P-Zn systems and its application to tribochemical reactions between ZnDTP-derived tribofilm and iron oxide,” Computational Material Science 231, 112550 (2024).

狭窄管内流れのFSI有限要素解析と造影剤動態解明

冠動脈の狭窄部の機能的重症度の有力な評価法として冠血流量予備量比（FFR, fractional flow reserve）が知られていますが、その測定にはカテーテルにより狭窄部の遠方まで圧測定用のガイドワイヤーを通過させる必要があり侵襲性が高いという問題があります。Transluminal contrast Attenuation Gradient（TAG）は冠動脈基部からの距離に対する造影剤の濃度勾配から機能評価を行う手法であり、侵襲性が低くかつ簡便な指標として期待されています。その指標の力学的根拠となる濃度勾配の形成メカニズム解明のためには、造影剤濃度の高い血液が噴流となり狭窄後の流体を交換する動態を考慮する必要があります。本研究では分岐狭窄柔軟ファントム拍動流実験とそれを模擬したALE流体構造連成解析を行い、更に狭窄率80%と95%において漸増する造影剤に見立てたパーティクルトレース解析を行いました。徐々に造影剤が充満する様子を可視化し、80%狭窄では軸対称な流れにより再現性のある密度分布を確認しました。一方で、95%狭窄では噴流の方向が変化することで密度分布が拍毎にばらつきが生じ、高狭窄率でのTAGの感度低下の原因となっている可能性を示しました。

動画は、流体構造連成解析結果とその流速場上での造影剤に見立てたパーティクルトレース解析結果です。流体は血液の粘性を仮定しており、入り口造影剤濃度を漸増させ、狭窄後部が徐々に造影剤で充満する様子を可視化しています。上から面積狭窄率80%、90%、95%の解析結果です。

参考文献

• 波田野 明日可，住吉谷 淳，鈴木 一真，牛流 章弘，加納 明，加藤 光章，廣畑 賢治，泉 聡志．「分岐狭窄柔軟ファントム実験とALE流体構造連成解析による造影剤動態解明」日本機械学会論文集 Vol.84, No.863 (2018)
  WEB

SiCの熱酸化

MOSFETなどの半導体デバイスの製造には、高品質な酸化膜の形成が不可欠です。ワイドギャップ半導体である炭化ケイ素(SiC)では、Si半導体と同様にSiO2酸化膜が作成できることから次世代パワー半導体の材料として注目されています。しかしながら、高品質なSiC/SiO2界面の製造は達成されておらず、特にSiCの面方位によって酸化の速度や品質が大きく異なるなどのSiCに特有の現象が実験的に報告されており、界面反応のメカニズムの原子論的な解明が待たれていました。一方、熱酸化による酸化膜成長というダイナミックな現象を扱うため、大規模な分子シミュレーションの適用が望まれていました。

本研究では、酸化プロセス再現のためのSi-O-C系の原子間ポテンシャルを新たに開発し、酸化膜成長のシミュレーションを行いました。ポテンシャル開発では、第一原理計算を使った小規模な酸化シミュレーションを教師データとし、合計1,000,000以上の物性値をフィッティングしました。SiC酸化シミュレーションでは数千原子・数ナノ秒オーダーでの酸化膜成長シミュレーションを行い、Si面の活性化エネルギーがC面の活性化エネルギーより大幅に大きいことを示しました。さらにSiの酸化数と活性化エネルギーの関係を調べることで、Si面ではSi1+を含む平坦な界面構造が作られ、これがSi面特有の高い活性化エネルギーの起源であることを提案しました。C面では対照的に、Si原子が引き上げられることで不規則な界面が形成されました。シミュレーションの結果から、C面では過剰なC原子がより多く生成されることも示唆されています。

参考文献

• So Takamoto, Takahiro Yamasaki, Takahisa Ohno, Chioko Kaneta, Asuka Hatano, and Satoshi Izumi, "Elucidation of the atomic-scale mechanism of the anisotropic oxidation rate of 4H-SiC between the (0001) Si-face and (000-1) C-face by using a new Si-O-C interatomic potential", Journal of Applied Physics 123, 185303 (2018).

心筋細胞の微細構造を考慮した電気生理・力学統合シミュレーション

生命維持をつかさどる心臓の機能は、心臓を構成する各心筋細胞の収縮により実現します。その心筋細胞は内部に規則正しい微細構造を持っています。心臓病などの病態細胞では生理的機能低下に加え、この構造が乱れることが知られていますが、病変との因果関係は推測の域を出ません。本研究では細胞内の3次元構造の影響を考慮し、電気生理・力学現象を統合したマルチフィジックス有限要素解析を実現しました。実験で得られる細胞の平均挙動とCa濃度分布の再現によりモデルの検証を行い[1]、T管の欠損による収縮動態の変化に関する検討[2]、ミトコンドリアとCa放出口の距離が代謝や収縮に及ぼす影響の検討[3]、ミトコンドリアの細胞内位置と虚血の関係に関する検討[4]等により細胞内の形態と心筋細胞の機能の関係について研究を行ってきました。分子生物学・ゲノミクスから得られた数多くの情報を有機的に結びつけ、医学・薬学への橋渡しとなるようなシミュレーションを目指しています。

心筋細胞内の構造の模式図(右)と有限要素モデル(左)

参考文献

• [1] Hatano et al. A 3-D simulation model of cardiomyocyte integrating excitation-contraction coupling and metabolism. Biophysical Journal, 101(11):2601-2610, 2011
• [2] Hatano et al. Critical role of cardiac t-tubule system for the maintenance of contractile function revealed by a 3D integrated model of cardiomyocytes. Journal of Biomechanics, 45(5):815-823, 2012
• [3] Hatano et al. Mitochondrial Colocalization with Ca2+ Release Sites is Crucial to Cardiac Metabolism. Biophysical Journal, 104(2):496-504, 2013
• [4] Hatano et al. Distinct Functional Roles of Cardiac Mitochondrial Subpopulations Revealed by a 3D Simulation Model. Biophysical Journal, 108(11):2732–2739, 2015

SBEM画像に基づく深層学習を用いた心筋細胞小器官のセグメンテーション手法の開発

心筋細胞内の小器官は，正常な細胞と心臓病をはじめとした病態の細胞との間で形態に差があることが知られています．しかし，小器官の形態の定量的な評価は，電子顕微鏡画像の手作業によるセグメンテーションに多大な時間を要するため，制限があります．形態異常と機能障害との関係性への理解を深めるために，電子顕微鏡画像から形態を再構築する手法の構築が望まれています．

本研究では，心筋細胞の連続断面を観察した電子顕微鏡画像（SBEM画像）から小器官の一つであるミトコンドリアを抽出・再構築する手法を開発しました．クラウドベースの深層学習ネットワークCDeep3Mを使用してミトコンドリア内部と境界をセグメンテーションしたのち，その結果を用いて画像処理を用いた後処理によってミトコンドリアを分離・再構築しました．セグメンテーション結果の指標の一つであるF値の最高値は約95％であり，手作業による結果と同等の結果が得られました．

この小器官の再構築手法は，多くの小器官の三次元形状を定量的に評価し，統計的な形状の議論を行うことを可能とします．また，心筋細胞の構造と機能との関係性の理解を深めるのに役立つと考えられます．

ミトコンドリアの実形状再構築手法の概略図

参考文献

• Asuka Hatano, Makoto Someya, Hiroaki Tanaka, Hiroki Sakakima, Satoshi Izumi, Masahiko Hoshijima, Mark Ellisman, Andrew D. McCulloch, “Isolation and reconstruction of cardiac mitochondria from SBEM images using a deep learning-based method”, Journal of Structural Biology, 214, 107806(2022)